Inteligência Artificial sem Magia: Como uma Rede Neural Realmente Aprende
1. Visão Geral: Chega de Magia, Vamos Falar de Mecânica
Se você já ouviu falar de Inteligência Artificial e imaginou uma caixa-preta mística que cospe respostas, você veio ao lugar certo. A verdade, como sempre, é muito mais interessante (e menos assustadora). Uma rede neural não é mágica; ela é um mecanismo. Um mecanismo surpreendentemente simples em suas partes, mas que exibe um comportamento complexo e poderoso quando essas partes trabalham juntas. Como destacado, "por trás de toda a complexidade e do hype, o que encontramos é... um mecanismo de tentativa e erro" (Maltempi, 2024).
A aplicação IA-Experience é sua bancada de testes. Ela foi criada para rasgar o véu e mostrar a engrenagem, a matemática e a lógica que movem o "aprendizado" de máquina. O objetivo aqui não é apenas ver a IA funcionar, mas sim entender por que ela funciona, colocando as mãos na massa, ajustando os parafusos e vendo o motor responder em tempo real. Esta abordagem se alinha com a literatura pedagógica que defende a visualização e a interação como catalisadores para o entendimento de sistemas complexos (Naps et al., 2002).
2. Os Blocos de Construção: Anatomia de uma Rede Neural
Antes de pilotar o avião, precisamos conhecer as peças. Uma rede neural, por mais complexa que pareça, é construída a partir de alguns componentes fundamentais.
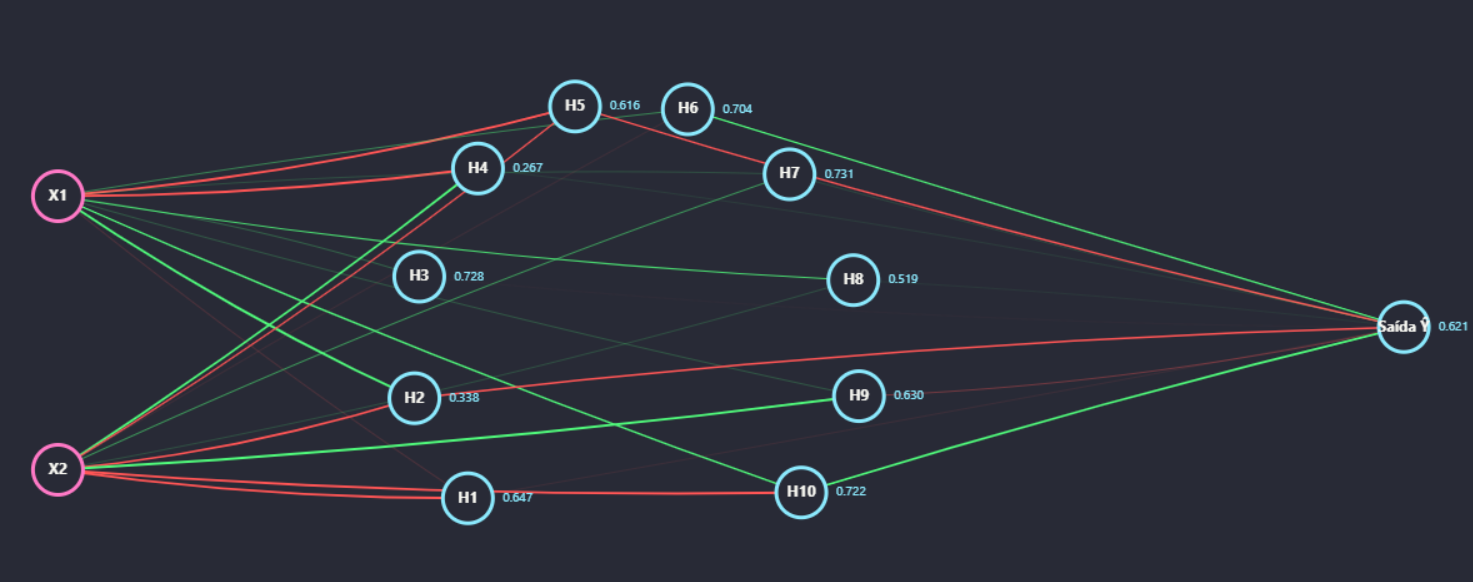
2.1. O Neurônio Artificial: O "Operário" da Rede
Pense em um neurônio como um único operário em uma linha de montagem. Ele tem uma tarefa muito específica: receber informações, tomar uma decisão simples com base nelas e passar o resultado adiante. Este conceito é a evolução direta do Perceptron, proposto por Frank Rosenblatt em 1958, que foi um dos primeiros modelos matemáticos de um neurônio.
Entradas (Inputs): São os dados brutos que chegam ao neurônio.
Pesos (Weights): Este é o conceito mais crucial. Um peso é um multiplicador que define a importância de uma entrada. Imagine que nosso operário (o neurônio) tem dois gerentes (as entradas). Se o peso da conexão com o Gerente 1 for alto, a opinião dele é muito importante. Se o peso for negativo, o operário faz o oposto do que aquele gerente diz. O "aprendizado" é, em essência, o processo de ajustar esses pesos.
Viés (Bias): O viés é um "empurrãozinho" extra. Pense nele como o humor ou a teimosia do nosso operário. É um valor fixo que é somado ao resultado das entradas ponderadas, permitindo que o neurônio seja mais flexível e não dependa exclusivamente das entradas para ser ativado.
Função de Ativação (Sigmoid): Depois de ouvir todas as entradas ponderadas e somar seu próprio viés, o neurônio precisa tomar sua decisão final. A função de ativação é a regra para essa decisão. Ela pega a soma total (que pode ser qualquer número) e a "esmaga" para dentro de um intervalo bem definido. Nossa simulação usa a Função Sigmoid, que sempre retorna um valor entre 0 e 1.
2.2. A Arquitetura: Montando a Fábrica
- Camada de Entrada (Input Layer): Por onde os dados brutos (
X1eX2) entram no sistema. - Camada Oculta (Hidden Layer): O coração da fábrica. Os neurônios desta camada recebem as informações da camada de entrada e começam a processá-las. Foi a dificuldade do Perceptron original em resolver problemas não-lineares, como o famoso "XOR", que demonstrou a necessidade de arquiteturas mais complexas com estas camadas intermediárias (Minsky & Papert, 1969).
- Camada de Saída (Output Layer): A camada final da rede. Ela recebe as informações processadas pela camada oculta e produz o resultado final, a predição da rede (
Ŷ).
3. O Motor do Aprendizado: Como a Rede "Pensa"
A rede não pensa. Ela calcula. O processo de "aprendizado" é um ciclo engenhoso de cálculo e ajuste, conhecido como Backpropagation (Retropropagação do Erro). Este algoritmo, popularizado por Rumelhart, Hinton & Williams (1986), foi o grande salto que permitiu o treinamento eficaz de redes com múltiplas camadas.
- O Chute (Feedforward): A rede processa as entradas com seus pesos e vieses atuais e produz uma predição.
- A Realidade (Cálculo do Erro): A predição é comparada com o valor alvo para ver o quão errada ela foi.
- O Detetive (Backpropagation): Um algoritmo que trabalha de trás para frente, calculando a "culpa" de cada neurônio pelo erro final.
- O Ajuste (Atualização): Com base na culpa, cada peso e viés é ajustado um pouquinho na direção certa para diminuir o erro na próxima vez. A Taxa de Aprendizado (
learningRateno código) controla o tamanho desse "passinho" de ajuste.
4. Mergulhando no Código (app.js)
Agora, vamos abrir o capô e ver como esses conceitos se transformam em código funcional.
4.1. A Célula Fundamental: A Classe Neuron
O conceito de neurônio é materializado em uma class no JavaScript. Ela é o "plano de construção" para cada operário da nossa rede.
class Neuron {
constructor(numInputs, name, position) {
this.name = name;
// 1. Pesos são inicializados com valores aleatórios entre -1 e 1
this.weights = Array.from({ length: numInputs }, () => Math.random() * 2 - 1);
// 2. Bias também é inicializado aleatoriamente
this.bias = Math.random() * 2 - 1;
this.output = 0;
// ...
}
// 3. A função de ativação Sigmoid
sigmoid = (x) => 1 / (1 + Math.exp(-x));
// 4. A derivada da Sigmoid (usada no backpropagation)
sigmoidDerivative = () => this.output * (1 - this.output);
// 5. O processo de FeedForward do neurônio
feedForward(inputs) {
const sum = inputs.reduce((acc, input, i) => acc + input * this.weights[i], this.bias);
this.output = this.sigmoid(sum);
return this.output;
}
}
- & 2 (Pesos e Bias): No
constructor, cada neurônio nasce sem saber de nada, com pesos e bias aleatórios, que é o ponto de partida para o aprendizado. - ** (Sigmoid):** Implementação matemática da função que "esmaga" a saída para um valor entre 0 e 1.
- ** (Derivada):** Essencial para o Backpropagation, ajuda a medir a "confiança" do neurônio em sua decisão para modular os ajustes.
- ** (FeedForward):** Executa a tarefa do "operário": recebe
inputs, multiplica-os pelosweights, soma obiase aplica asigmoidpara gerar aoutputfinal.
4.2. A Fábrica em Ação: O Backpropagation
A função backpropagateNetwork é o motor do aprendizado, executando o ciclo de treinamento a cada clique no botão "Treinar".
function backpropagateNetwork(inputs, targetVal) {
// PASSO 1: O CHUTE (Feedforward)
const hiddenOutputs = hiddenLayer.map(n => n.feedForward(inputs));
const predictedOutput = outputNeuron.feedForward(hiddenOutputs);
// PASSO 2: A REALIDADE (Cálculo do Erro)
const error = targetVal - predictedOutput;
// PASSO 3: O DETETIVE (Backpropagation)
outputNeuron.delta = error * outputNeuron.sigmoidDerivative(); // Culpa da saída
hiddenLayer.forEach((hiddenN, hIndex) => { // Distribuição da culpa
hiddenN.delta = outputNeuron.delta * outputNeuron.weights[hIndex] * hiddenN.sigmoidDerivative();
});
// PASSO 4: O AJUSTE (Atualização dos Pesos e Vieses)
outputNeuron.weights.forEach((w, i) => {
outputNeuron.weights[i] += learningRate * outputNeuron.delta * hiddenOutputs[i];
});
outputNeuron.bias += learningRate * outputNeuron.delta;
hiddenLayer.forEach((hiddenN) => { // Ajuste da camada oculta
hiddenN.weights.forEach((w, iIndex) => {
hiddenN.weights[iIndex] += learningRate * hiddenN.delta * inputs[iIndex];
});
hiddenN.bias += learningRate * hiddenN.delta;
});
}
Este bloco de código é a tradução literal do algoritmo. O error é usado para calcular o delta (a culpa), que por sua vez é usado para ajustar os weights e bias de cada neurônio, sempre modulado pela learningRate.
4.3. A Bancada de Testes: O Modo de Simulação de Neurônio
A função switchToNeuronView é a alma da proposta interativa da ferramenta, permitindo isolar e manipular um único neurônio diretamente.
function switchToNeuronView() {
simulationMode = 'neuron'; // Muda o modo da aplicação
// ...
// Para cada PESO do neurônio selecionado, cria um slider de controle
selectedNeuron.weights.forEach((weightValue, i) => {
// ...
slider.addEventListener('input', (e) => {
// Atualiza o peso do neurônio em TEMPO REAL com o valor do slider
selectedNeuron.weights[i] = parseFloat(e.target.value);
simulateSingleNeuron(); // Recalcula a saída do neurônio imediatamente
// ...
});
});
// ... (código similar para o Bias)
}
Quando você arrasta um slider nesta visão, o código altera a propriedade selectedNeuron.weights e imediatamente recalcula a saída, criando uma conexão direta e intuitiva entre a causa (o valor do peso) e o efeito (a saída do neurônio).
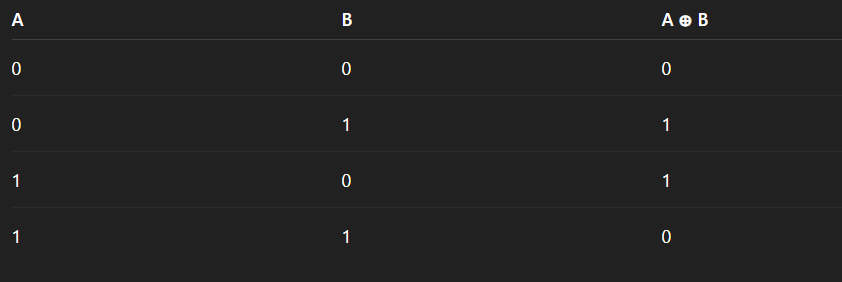
Amostra de Teste: Ensinando a Rede a "Pensar" com a Lógica XOR
A teoria é fundamental, mas a verdadeira compreensão emerge da prática. Proponho um desafio clássico para nossa rede: ensiná-la a operar como uma porta lógica XOR (OU Exclusivo). Este problema é fascinante porque, embora simples, sua solução não é linear – um neurônio sozinho jamais conseguiria resolvê-lo, exigindo uma camada oculta.
O Desafio:
A rede deve aprender as seguintes regras:
- Se a
`Entrada 1`E a`Entrada 2`forem 0, a Saída deve ser 0. - Se a
`Entrada 1`for 0 e a`Entrada 2`for 1, a Saída deve ser 1. - Se a
`Entrada 1`for 1 e a`Entrada 2`for 0, a Saída deve ser 1. - Se a
`Entrada 1`E a`Entrada 2`forem 1, a Saída deve ser 0.
Passo a Passo no Cérebro Neural Interativo:
- Configuração Inicial: No painel, ajuste o número de
`Neurônios na Camada Oculta`para, no mínimo, 2. Um único neurônio não consegue aprender o padrão XOR. - Primeiro Treino (0, 0 → 0):
- No painel, ajuste o slider
`Entrada (X1)`para 0.00 e`Entrada (X2)`para 0.00. - Ajuste o slider
`Saída Desejada (Y)`para 0.00. - Observe a
`Saída (Ŷ)`inicial da rede. Será um valor aleatório. O`Erro`será a diferença entre este valor e 0.00. - Clique no botão "Treinar Rede" uma vez. Observe como os pesos (as linhas) mudam sutilmente de cor e espessura. A rede fez seu primeiro ajuste.
- No painel, ajuste o slider
- Ciclos de Treinamento Iterativo: O aprendizado requer repetição. Agora, treine a rede nos outros três casos:
- Ajuste as entradas para
`X1=0.00`,`X2=1.00`e a saída desejada`Y=1.00`. Clique em "Treinar Rede" algumas vezes. - Ajuste para
`X1=1.00`,`X2=0.00`e`Y=1.00`. Clique em "Treinar Rede" mais algumas vezes. - Ajuste para
`X1=1.00`,`X2=1.00`e`Y=0.00`. Clique em "Treinar Rede" novamente.
- Ajuste as entradas para
- Observação da Convergência: Continue alternando entre os quatro cenários e clicando em "Treinar Rede". Você notará que o valor do
`Erro`geral começa a diminuir drasticamente. Após dezenas de cliques, a rede começará a prever corretamente a saída para cada par de entradas. Ela aprendeu o padrão XOR.
A Anatomia do Aprendizado: Interpretando o Gráfico
Após os ciclos de treino, clique em "Ver Gráfico de Aprendizado". A imagem que você verá é, em essência, a prova visual de que a inteligência emergiu da matemática.
Dissecando o Gráfico:
- Eixo Horizontal (Ciclos de Treino): Representa o tempo e a experiência. Cada ponto neste eixo é um momento em que a rede foi corrigida.
- Eixo Vertical (Erro Médio): Representa a "ignorância" ou a "dor" da rede. Quanto mais alto, mais longe suas respostas estão do alvo.
- A Curva Descendente: Este é o backpropagation em ação. A queda inicial, geralmente acentuada, mostra a rede fazendo grandes correções em seus pesos. À medida que a curva se suaviza, a rede está fazendo ajustes finos, refinando seu conhecimento.
- A Estabilização (Platô): Quando a curva se achata perto de zero, significa que a rede convergiu. Ela encontrou uma combinação de pesos e biases que resolve o problema de forma satisfatória. Treinos adicionais trarão retornos cada vez menores. A rede aprendeu.
5. Legenda de Termos (Glossário)
Para ajudar a desmistificar o jargão, aqui está uma tradução de alguns dos termos e metáforas usados nesta documentação.
"Culpa" / "Distribuindo a Culpa"
- O que é na prática: É uma metáfora para o conceito matemático de "contribuição para o erro".
- Explicação: Quando a rede erra, o algoritmo backpropagation calcula o quanto cada neurônio e cada peso individualmente "colaboraram" para esse erro. A "culpa" é um valor numérico (chamado de Delta ou Gradiente) que representa: "Se alterarmos este peso ou este viés, o quanto o erro final irá diminuir?". Distribuir a culpa é o processo de calcular esse valor para todos os componentes, de trás para frente.
Backpropagation (Retropropagação do Erro)
- O que é na prática: O algoritmo central que permite o treinamento da rede.
- Explicação: É o "motor do aprendizado". Depois que a rede faz uma previsão e o erro é calculado, o backpropagation é o método que propaga essa informação de erro de volta pela rede (da camada de saída para a de entrada) para descobrir como ajustar os pesos e vieses de forma a cometer um erro menor na próxima tentativa.
Convergência
- O que é na prática: O processo da rede se tornar cada vez mais precisa durante o treinamento.
- Explicação: Dizemos que a rede está "convergindo" quando suas previsões (a linha verde no nosso gráfico) estão ficando consistentemente mais próximas dos valores-alvo (a linha amarela). É o sinal de que o aprendizado está funcionando e o erro está diminuindo.
Delta
- O que é na prática: O valor numérico calculado que representa a "culpa" de um neurônio.
- Explicação: Para cada neurônio, o
Deltaé o resultado do cálculo que combina o erro da camada seguinte com a própria saída do neurônio. Ele serve como a principal instrução para o ajuste: umDeltagrande significa que aquele neurônio precisa de um ajuste significativo.
Feedforward (Avanço Direto)
- O que é na prática: O processo de fazer uma previsão.
- Explicação: Refere-se ao fluxo de informações se movendo em uma única direção – da camada de entrada, passando pelas camadas ocultas, até a camada de saída – para gerar um resultado. É o "chute" ou a "opinião" da rede com base em seus pesos e vieses atuais.
Função de Ativação (Sigmoid)
- O que é na prática: Uma função matemática aplicada à saída de um neurônio.
- Explicação: É a regra de "decisão" do neurônio. Ela pega a soma total das entradas ponderadas (que pode ser qualquer número, como 5.7 ou -10.2) e a comprime para dentro de um intervalo previsível (no caso da Sigmoid, entre 0 e 1). Isso ajuda a rede a lidar com relações complexas e não-lineares nos dados.
Não-linear
- O que é na prática: Um padrão ou problema que não pode ser resolvido ou separado por uma única linha reta.
- Explicação: Imagine tentar separar pontos pretos e brancos em um gráfico. Se você consegue fazer isso com uma única régua, o problema é linear. O problema "XOR" é famoso por ser não-linear, pois você precisa de mais de uma linha para separar as saídas corretamente. As funções de ativação dão às redes neurais a capacidade de "dobrar" e "torcer" suas decisões, permitindo que elas resolvam esses problemas complexos.
Pesos (Weights)
- O que é na prática: Um número que representa a força de uma conexão entre neurônios.
- Explicação: É a variável mais importante da rede. Um peso alto significa que a informação vinda daquela conexão é muito relevante. Um peso baixo significa que é pouco relevante. Um peso negativo inverte o sinal da informação. O treinamento consiste, fundamentalmente, em encontrar os valores de peso perfeitos para resolver um problema.
Taxa de Aprendizado (Learning Rate)
- O que é na prática: Um parâmetro que controla a velocidade do treinamento.
- Explicação: Após o algoritmo calcular o ajuste necessário para um peso ("a culpa"), a taxa de aprendizado determina o tamanho do passo que daremos nessa direção. É um ajuste fino: um passo muito grande pode fazer com que a rede nunca encontre a melhor solução, enquanto um passo muito pequeno pode tornar o treinamento extremamente lento.
Viés (Bias)
- O que é na prática: Um valor numérico adicionado à soma ponderada das entradas de um neurônio.
- Explicação: Pense nele como o "ponto de partida" de um neurônio. Sem um viés, se todas as entradas fossem zero, a saída também seria sempre zero. O viés dá ao neurônio uma espécie de "teimosia" ou tendência inata, permitindo que ele se ative mesmo com entradas fracas (se o viés for alto e positivo) ou que precise de um estímulo muito forte para se ativar (se o viés for alto e negativo).
6. Referências
Cérebro Neural Interativo: https://clarkmaltempi.github.io/IA-Experience/
Maltempi, C. (2024). O Fim do Hype: O Que a IA Realmente Significa Para Sua Carreira. Projeto Plataforma.
Minsky, M., & Papert, S. (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press.
Naps, T. L., et al. (2002). Exploring the role of visualization and engagement in computer science education. ACM SIGCSE Bulletin.
Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review.
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.