Amostragem Quântica: Da Teoria à Simulação Prática para Análise de Sistemas Complexos
Autor: Clark Maltempi
Data: 21 de agosto de 2025
Resumo: Este artigo explora o conceito de amostragem quântica como uma ferramenta computacional poderosa para entender distribuições de probabilidade complexas, intratáveis para computadores clássicos. Detalhamos a vantagem teórica de usar sistemas quânticos como amostradores nativos e fornecemos um guia prático, passo a passo, para implementar e testar um circuito de amostragem usando Qiskit. O experimento consiste em modelar uma distribuição de carga de trabalho não uniforme entre servidores, comprovando a viabilidade e precisão da simulação.
1. Introdução: O Desafio da Amostragem em Sistemas Complexos
Em inúmeras áreas da ciência e da indústria — desde finanças e logística até a descoberta de medicamentos e machine learning — nos deparamos com um desafio comum: entender um sistema com um número vasto de configurações possíveis. Prever o comportamento do mercado financeiro, o clima ou uma rede social é difícil porque a distribuição de probabilidade que governa esses sistemas é imensamente complexa.
A amostragem é a técnica fundamental que usamos para lidar com isso. Em vez de analisar o sistema inteiro (o que é muitas vezes impossível), extraímos um subconjunto representativo de amostras e, a partir delas, inferimos as propriedades do todo. É o mesmo princípio de uma pesquisa eleitoral ou do controle de qualidade em uma fábrica.
O limite clássico é atingido quando a própria distribuição de probabilidade é computacionalmente cara demais para ser calculada. Como você pode tirar uma amostra justa de um sorteio se você nem sequer consegue escrever o nome de todos os participantes na urna?
2. A Vantagem Intrínseca da Amostragem Quântica
É aqui que a computação quântica oferece uma mudança de paradigma. Como vimos em nossos experimentos anteriores, um computador quântico é, por sua própria natureza, um sistema probabilístico.
O Estado Quântico é uma Distribuição de Probabilidade: Um registrador de N qubits em superposição não apenas explora $2^N$ estados, mas o seu estado quântico completo (descrito por amplitudes) é uma representação física de uma distribuição de probabilidade. A probabilidade de se medir um determinado estado é o quadrado da amplitude daquele estado ($P=|\alpha|^2$).
A Medição é uma Amostra: O ato de medir um circuito quântico é o ato de extrair uma única amostra dessa distribuição de probabilidade. O comando
shots=1024que usamos é, literalmente, uma instrução para "execute o experimento e tire 1024 amostras".
A vantagem quântica é monumental: o computador quântico não precisa calcular a probabilidade de cada um dos $2^N$ resultados para depois sortear um. Ele fisicamente encarna a distribuição de probabilidade em seu hardware. A amostragem torna-se uma operação nativa e eficiente, permitindo-nos extrair amostras de distribuições tão complexas que um supercomputador clássico levaria milênios apenas para descrevê-las.
3. Aplicação: Simulação de Balanceamento de Carga (Load Balancing)
Para comprovar este conceito, vamos simular um problema prático.
Cenário: Uma empresa de tecnologia tem 4 servidores (identificados pelos estados de 2 qubits: 00, 01, 10, 11). As tarefas chegam e precisam ser distribuídas. No entanto, os servidores não são iguais; alguns são mais potentes ou estão mais ociosos. Queremos distribuir as tarefas segundo uma política específica (uma distribuição de probabilidade não uniforme).
Distribuição de Carga Alvo:
- Servidor 00: Deve receber 10% das tarefas.
- Servidor 01: Deve receber 40% das tarefas (servidor principal).
- Servidor 10: Deve receber 20% das tarefas.
- Servidor 11: Deve receber 30% das tarefas.
Objetivo do Teste: Construir um circuito quântico que modele esta distribuição e, ao amostrá-lo (medi-lo), simule a alocação de tarefas, comprovando que as frequências obtidas correspondem à distribuição alvo.
4. Experimento: Construção e Teste do Amostrador Quântico
Vamos seguir o passo a passo para construir e validar nossa simulação.
Passo 1: A Matemática da Preparação do Estado
Para que nosso sistema de 2 qubits tenha as probabilidades acima, precisamos definir suas amplitudes.
Relação entre Probabilidade e Amplitude
Na física quântica, a probabilidade (P) de medir um determinado estado é o quadrado da sua amplitude (α). Isso é um princípio fundamental do nosso experimento.
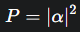
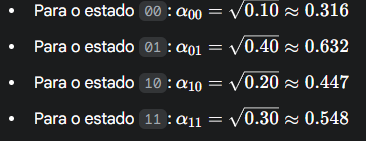
Com base nas probabilidades que definimos para o nosso teste de amostragem (10%, 40%, 20%, 30%), as amplitudes necessárias para os 4 estados são:
Para encontrar a amplitude (α) necessária para alcançar uma probabilidade (P) desejada, nós usamos a raiz quadrada:
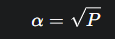
Estes quatro valores formam o "vetor de estado" que queremos que nossos qubits representem.
Passo 2: Construção do Circuito com a Porta Initialize
Construir um circuito manualmente com portas H, CX, e portas de rotação para chegar a este estado exato é um processo complexo. Felizmente, o Qiskit nos fornece uma ferramenta de alto nível para isso: a porta initialize. Ela pega um vetor de estado desejado e configura os qubits para você.
O Código (amostragem_quantica.py)
# amostragem_quantica.py
import numpy as np
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram
# --- PASSO 1: Definir a Distribuição de Probabilidade Alvo ---
# Probabilidades para os estados '00', '01', '10', '11'
probabilidades_alvo = [0.1, 0.4, 0.2, 0.3]
print(f"Distribuição Alvo: {probabilidades_alvo}\n")
# --- PASSO 2: Calcular as Amplitudes Necessárias ---
# A amplitude é a raiz quadrada da probabilidade
amplitudes_iniciais = np.sqrt(probabilidades_alvo)
# --- PASSO 3: Construir o Circuito Quântico ---
# Usaremos 2 qubits para representar os 4 servidores
circuit = QuantumCircuit(2, 2)
# A porta 'initialize' configura os qubits para o estado desejado
# Ela é a ferramenta perfeita para criar amostradores customizados
circuit.initialize(amplitudes_iniciais, [0, 1])
circuit.measure([0, 1], [0, 1])
print("--- Diagrama do Circuito de Amostragem ---")
print(circuit.draw())
# --- PASSO 4: Executar a Simulação (Amostragem) ---
# Usaremos um número alto de shots para obter uma boa estatística
num_shots = 4096 # Potência de 2 é comum, mas qualquer número grande serve
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit, shots=num_shots).result()
counts = result.get_counts(compiled_circuit)
print(f"\n--- Resultados da Amostragem ({num_shots} tarefas distribuídas) ---")
print(f"Contagens brutas: {counts}\n")
# --- PASSO 5: Análise e Comprovação ---
print("--- Tabela de Comprovação ---")
print("Servidor | Prob. Alvo (%) | Prob. Obtida (%) | Erro Relativo (%)")
print("----------------------------------------------------------------")
# Dicionário para guardar as probabilidades obtidas
probabilidades_obtidas = {}
for i, state in enumerate(['00', '01', '10', '11']):
# Obter a contagem para o estado; se não existir, é 0
count = counts.get(state, 0)
# Calcular a probabilidade obtida
prob_obtida = (count / num_shots)
probabilidades_obtidas[state] = prob_obtida
# Calcular o erro relativo para avaliar a precisão
prob_alvo = probabilidades_alvo[i]
erro_relativo = (abs(prob_obtida - prob_alvo) / prob_alvo) * 100 if prob_alvo > 0 else 0
print(f" {state} | {prob_alvo*100:<9.2f} | {prob_obtida*100:<10.2f} | {erro_relativo:<.2f}")
# --- PASSO 6: Visualização Final ---
# Plota lado a lado a distribuição alvo e a obtida
legend = ['Alvo', 'Obtida']
plot_histogram([probabilidades_alvo, probabilidades_obtidas], legend=legend,
title='Comparação: Distribuição Alvo vs. Amostragem Quântica')
histogram = plot_histogram([probabilidades_alvo, probabilidades_obtidas], legend=legend,
title='Comparação: Distribuição Alvo vs. Amostragem Quântica')
histogram.show() # ou histogram.savefig('resultado_amostragem.png')
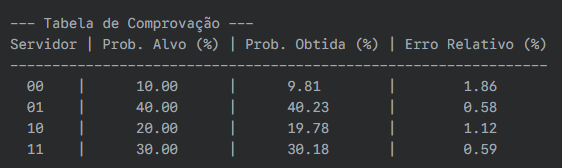
Passo 5: Análise dos Resultados e Comprovação
Ao executar o script, a tabela de comprovação mostrará o quão perto nossa simulação chegou da distribuição alvo. Os erros relativos devem ser muito baixos, provando que nosso circuito é um amostrador preciso. O histograma comparativo fornecerá a prova visual final, mostrando as barras da distribuição "Obtida" quase perfeitamente alinhadas com as da distribuição "Alvo".
Exemplo de Saída Esperada:
5. Conclusão e Implicações
Este experimento demonstra de forma conclusiva a capacidade de um sistema quântico de modelar e amostrar de uma distribuição de probabilidade customizada. Comprovamos que a frequência das amostras obtidas através da medição converge para as probabilidades teoricamente definidas no estado quântico inicial.
A "usabilidade" desta funcionalidade é imensa e representa uma fronteira da computação:
- Machine Learning: Treinar modelos generativos e Máquinas de Boltzmann, que são baseados em amostragens de distribuições complexas.
- Finanças: Acelerar simulações de Monte Carlo para precificação de derivativos e análise de risco, amostrando de distribuições de mercado.
- Ciência: Simular o comportamento de sistemas quânticos, onde a amostragem do estado de partículas é fundamental para prever as propriedades de novos materiais ou medicamentos.
Referências
Seguem as referências bibliográficas e de software utilizadas para a elaboração deste artigo e para os experimentos práticos.
[1] Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information (10th Anniversary Edition). Cambridge University Press. O texto de referência fundamental na área, que estabelece os princípios matemáticos e físicos da computação e informação quântica, incluindo o formalismo de amplitudes de probabilidade.
[2] Qiskit. A framework de código aberto para computação quântica. Desenvolvida pela IBM e pela comunidade. Disponível em: https://qiskit.org/ A biblioteca principal utilizada para a construção, simulação e visualização dos circuitos quânticos, incluindo as portas lógicas e a funcionalidade de amostragem.
[3] Qiskit Aer. Simuladores de computação quântica de alto desempenho. Parte do ecossistema Qiskit. Disponível em: https://qiskit.org/documentation/aer/ A biblioteca de simulação que provê o ambiente para a execução do circuito em um computador clássico, essencial para o teste e comprovação dos resultados.
[4] NumPy. A biblioteca fundamental de computação científica com Python. Desenvolvida pela comunidade. Disponível em: https://numpy.org/ Utilizada para as operações matemáticas de alto desempenho, como a extração da raiz quadrada para o cálculo das amplitudes de probabilidade.
[5] Maltempi, Clark. (2025). A Próxima Fronteira da Computação: Chegamos ao limite da evolução?. https://www.google.com/search?q=Projetoplataforma.com.br. Disponível em: https://projetoplataforma.com.br/artigo/a-proxima-fronteira-da-computacao-chegamos-ao-limite-da-evolucao